Ecuaciones Diferenciales.: 4. Sistema de Ecuaciones Diferenciales

4. Sistema de Ecuaciones Diferenciales

Un sistema de ecuaciones diferenciales es un conjunto de varias Ecuaciones Diferenciales con varias funciones incógnitas y un conjunto de condiciones de contorno. Una solución del mismo es un conjunto de funciones diferenciables que satisfacen todas y cada una de las ecuaciones del sistema. Según el tipo de ecuaciones diferenciales pude tenerse un sistema de ecuaciones diferenciales ordinarias o un sistema de ecuaciones en derivadas parciales.

Se expresa de la siguiente forma:

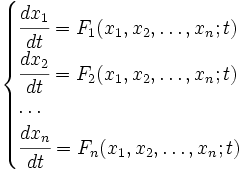
$\begin{cases} \cfrac{dx_1}{dt} = F_1(x_1,x_2,\ldots,x_n;t)\\ \cfrac{dx_2}{dt} = F_2(x_1,x_2,\ldots,x_n;t)\\ \ldots \\ \cfrac{dx_n}{dt} = F_n(x_1,x_2,\ldots,x_n;t) \end{cases}$

Reducción a un sistema de primer orden

Dado un sistema de ecuaciones diferenciales de orden n con m ecuaciones:

$F_i\left(x_j,\frac{dx_j}{dt},\ldots,\frac{d^nx_i}{dt^n};t\right) =0 \qquad \mbox{con}\ i,j\in\{1,2,\ldots,m\}$

Existe un sistema equivalente de primer orden con a lo sumo (n+1)xm ecuaciones. Para ver esto consideremos un sistema en que intervienen m funciones incógnitas x_i y sus n derivadas, e introduzcamos un nuevo conjunto de variables y_i,k definidos de la siguiente manera:

$y_{i,k}(t) := \frac{d^k x_i(t)}{dt^k}$

El sistema de primer orden equivalente en las variables y_i,k resulta ser:

$\begin{cases} y_{i,k+1} = \cfrac{dy_{i,k}}{dt} & k\in\{0,2,\ldots,n-1\}\\ F_i\left(y_{j,0},y_{j,1},\ldots,y_{j,n};t\right) =0 & i,j\in\{1,2,\ldots,m\} \end{cases}$

Ecuaciones Diferenciales.

lunes, 25 de junio de 2012

4. Sistema de Ecuaciones Diferenciales

Reducción a un sistema de primer orden

No hay comentarios:

Publicar un comentario